Kì thi AMO – Kì thi Toán học Hoa Kì

Kì thi AMO (American Math Olympiad) là một trong những cuộc thi Toán quốc tế lâu đời và uy tín dành cho học sinh tiểu học, trung học cơ sở và trung học phổ thông. Ở khu vực ASEAN và Hong Kong, kì thi được Trung tâm Olympic toán quốc tế của Singapore (SIMCC) và Đại học Nam Illinois (SIU) phối hợp tổ chức.
Đặc biệt, năm 2024 SIMCC sẽ hợp tác cùng Khoa Khoa học Liên ngành – Trường Đại học Khoa học Xã hội và Nhân văn – Đại học Quốc gia TP.HCM (FIS-USSH) tổ chức kì thi AMO ngay tại Việt Nam.
Tổng quan về kì thi Toán học Hoa Kì – AMO
Đối tượng dự thi
Học sinh từ lớp 2 đến lớp 12
Cấu trúc đề thi
| Ngôn ngữ | Thời gian | Phần | Số câu | Mức điểm | Phân loại |
| Tiếng Anh | 90 phút | A | 15 | 3 điểm/câu | Câu hỏi trắc nghiệm |
| B | 5 | 5 điểm/câu | Điền đáp số | ||
| C | 5 | 6 điểm/câu | Điền đáp số |
Quy định kì thi
- Học sinh chỉ ghi đáp án vào phiếu trả lời (không trình bày lời giải)
- Học sinh không được dùng máy tính
- Học sinh được phép sử dụng sách từ điển
Cơ cấu giải thưởng
- Huy chương vàng : Top 8% có điểm cao nhất
- Huy chương bạc : Top 12% có điểm cao tiếp theo
- Huy chương đồng : Top 20% có điểm cao tiếp theo
- Giải khuyến khích : Top 10% có điểm cao tiếp theo
- Giấy chứng nhận : Các thí sinh còn lại
ĐẶC BIỆT:
- Giải thưởng đặc biệt dành tặng thí sinh đạt điểm tối đa
- Học bổng dành tặng thí sinh đứng đầu mỗi khối lớp
Kì thi AMO 2024 tại Việt Nam
Lịch thi tại Việt Nam
- Thời gian: Chủ nhật, ngày 27/10/2024
- Khung giờ: 14:30 – 16:00
Địa điểm thi (dự kiến)
TP. Hồ Chí Minh, Hà Nội, Hải Phòng, Đà Nẵng, Quảng Ngãi, Gia Lai, Quảng Ninh, Huế, Vũng Tàu, Vĩnh Phúc
Cách thức đăng kí
Đăng kí trước ngày 23/9/2024
Lệ phí: 450.000 VNĐ/học sinh
Phụ huynh và học sinh đăng kí tham dự kì thi Toán học Hoa Kì 2024
Lợi ích khi tham gia kì thi
- Nâng cao năng lực Toán và tiếng Anh: Với đề thi hoàn toàn bằng tiếng Anh, học sinh sẽ được làm quen với ngôn ngữ học thuật, nâng cao vốn từ vựng môn Toán và rèn luyện được kĩ năng đọc hiểu. Đồng thời đây là cơ hội để học sinh rèn luyện khả năng tư duy toán học, giải quyết các bài toán sáng tạo và nâng cao kĩ năng tính toán.
- Đánh giá năng lực Toán học: Thông qua bài thi, học sinh sẽ được đánh giá năng lực Toán học một cách toàn diện và khách quan, giúp xác định điểm mạnh, điểm yếu từ đó đưa ra được định hướng học tập hiệu quả.
- Học bổng hấp dẫn: thí sinh tham dự và đạt giải tại kì thi AMO sẽ được Đại học Southern Illinois (SIU) của Mĩ trao tặng nhiều học bổng đại học có giá trị.
- Phát triển khả năng tư duy logic: Qua quá trình làm bài, học sinh sẽ rèn luyện khả năng suy luận, phân tích vấn đề một cách logic và hệ thống.
- Rèn luyện kĩ năng giải quyết vấn đề: Cấu trúc đề thi và các câu hỏi của AMO không chỉ đánh giá kiến thức mà còn tập trung vào khả năng vận dụng kiến thức để giải quyết các tình huống toán học.
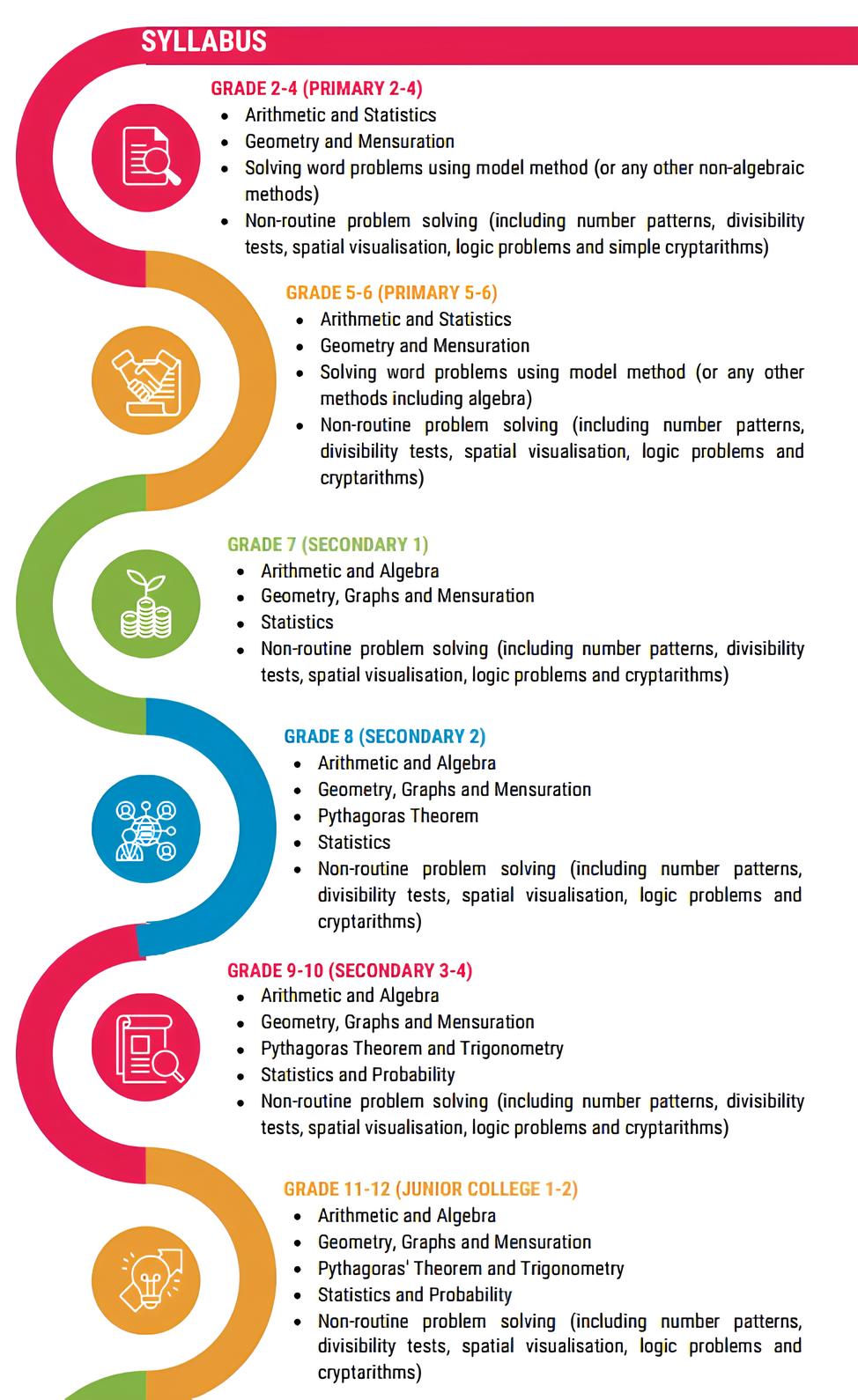
Nội dung ôn tập và dự thi kì thi AMO 2024
| Lớp | Nội dung |
| 2 | – 4 phép tinh cơ bản – Thống kê cơ bản (bài toán đếm, đọc biểu đồ,..)- Chu vi – Diện tích – Bài toán có lời văn – Bài toán quy luật – Bài toán tưởng tượng không gian đơn giản – Bài toán suy luận logic – Toán tự |
| 3 | |
| 4 | |
| 5 | – Các phép tính cơ bản – Thống kê cơ bản – Phép chia hết – Phép chia có dư – Chu vi – Diện tích – Thể tích – Bài toán quy luật (hinh & số) – Bài toán tường tượng không gian – Bài toán suy luận logic – Toán tự – Bài toán tổng-ti, tống-hiệu, hiệu-ti – Đại số (mức độ cơ bản) |
| 6 | |
| 7 | – Các phép tính với số thực – Phương pháp đại số và ứng dụng – Phép chia hết – Phép chia có dư – Đồ thị, hình học & đo lường – Đồ thị – Bài toán quy luật – Bài toán tưởng tượng không gian – Bài toán suy luận logic – Toán tự – Thống kê cơ bản |
| 8 | – Các phép tính với số thực – Phương pháp đại số và ứng dụng – Phép chia hết – Phép chia có dư – Đồ thị, hình học & đo lường – Định lý Pythagoras – Bài toán quy luật – Bài toán tưởng tượng không gian – Bài toán suy luận logic – Toán tự – Thống kê cơ bản |
| 9 | – Các phép tính với số thực – Phương pháp đại số và ứng dụng – Phép chia hết – Phép chia có dư – Đồ thị, hình học & đo lường – Định lí Pythagoras – Tỉ số lượng giác của góc nhọn – Bài toán quy luật – Bài toán tưởng tượng không gian – Bài toán suy luận logic – Toán tự – Thống kê & xác suất cơ bản |
| 10 | – Các phép tính với số thực – Phương pháp đại số và ứng dụng- Phép chia hết – Phép chia có dư – Đồ thị, hình học & đo lường – Định lí Pythagoras – Lượng giác cơ bản – Bài toán quy luật – Bài toán tưởng tượng không gian – Bài toán suy luận logic – Toán tự – Thống kê & xác suất cơ bản |
| 11 | – Các phép tính với số thực – Phương pháp đại số và ứng dụng – Phép chia hết – Phép chia có dư – Đồ thị, hình học & đo lường – Định lí Pythagoras – Lượng giác – Bài toán quy luật – Bài toán tưởng tượng không gian – Bài toán suy luận logic – Toán tự – Thống kê & xác suất cơ bản |
| 12 |
Bài Viết Phổ Biến






















